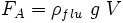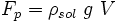Introduzione a Spinta di Archimede
Lo scopo di questa estensione e' quello di dare delle indicazioni di
massima sulla spinta di galleggiamento
della bombola. Quanti di voi si sono mai chiesti se alla fine
dell'immersione saremmo positivi o negativi?
Personalmente me lo sono chiesto tutte le volte che ho
pianificato una lunga immersione fuori curva.
E'
vero che se facciamo una buona pianificazione non dovremmo avere di
questi problemi ma e' altrettanto vero che gli imprevisti sono sempre
dietro l'angolo.
Gruppo Dati
Dati
In questo gruppo si inseriscono dati necessari per il calcolo della spinta di galleggiamento
- Litraggio
Bombola = A quanti litri corrisponde la Bombola
valore espresso in Litri - Pressione
Bar = A quanti Bar viene caricata la Bombola
valore espresso in Bar - Frazione
O2 = Corrisponde alla percentuale di Ossigeno nella
Bombola ( l'ossigeno ha una massa diversa da quella dell'Azoto)
valore espresso in % - Peso
Bombola = Quanto pesa la Bombola ( solo la
bombola senza rubinetteria)
valore espresso in Kg - Peso
Rubinetteria = Quanto pesa la rubinetteria della
Bombola
valore espresso in Kg - Temperatura
Gas = Temperatura del gas nella Bombola
valore espresso in gradi Celsius C - Volume
esterno della Bombola = Qual'è' il volume
esterno della Bombola
valore espresso in m^3
NOTA:
Se non si conosce il volume lo si può calcolare richiamando il Gruppo Volume Bombola
-
Densità' dell'acqua = Selezionare se
l'immersione e' in acqua dolce o salata.
| <<< Indietro |
Gruppo Simulatore
Simulatore
In questo gruppo e' possibile simulare la pressione della bombola trascinando la barra di
scorrimento.
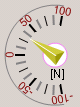
- E' possibile visualizzare la pressione in bombola
- E' possibile visualizzare forza di galleggiamento
La bombola Affonda. La lancetta e' Blu
.
La bombola e' neutra. La lancetta e' Verde

La bombola Galleggia. La lancetta e' Gialla
| <<< Indietro |
Gruppo Volume Bombola
II gruppo Volume bombola e' accessibile solo facendo clic sull'icona
 .
.Dopo il click il modulo si allarga verso destra e mette in luce una serie di nuovi parametri.
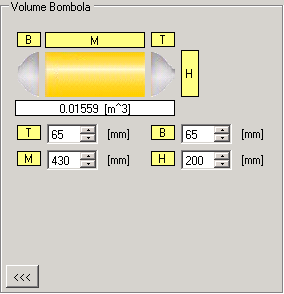
Orizzontalmente la Bombola e' suddivisa in 3 parti B = Fondo della bombola M = Parte centrale della bombola T = Parte frontale della bombola Verticalmente la bombola ha una sola parte H = Altezza della bombola ( il diametro) Tutte le misure sono espresse in millimetri. Ad ogni variazione delle caselle numeriche viene ricalcolato il volume esterno della bombola. Il risultato viene riportato nell'etichetta bianca sotto la bombola. In basso a sinistra il bottone con le 3 frecce <<< nasconde il Gruppo "Volume Bombola" |
 |
|
| <<< Indietro |
Storia
| Il principio di Archimede sul galleggiamento dei corpi | ||||
|
Sui corpi galleggianti è una delle principali opere di Archimede, nella quale viene fondata la scienza dell'idrostatica. Nel primo dei due volumi dell'opera si enuncia un postulato dal quale viene dedotto come teorema quello che oggi è impropriamente chiamato il principio di Archimede. Oltre a calcolare le posizioni di equilibrio statico dei galleggianti, si dimostra che l'acqua degli oceani, in condizioni di equilibrio, assume una forma sferica. Sin dall'epoca di Parmenide gli astronomi greci sapevano che la Terra fosse sferica, ma qui, per la prima volta, questa forma viene dedotta da principi fisici. Il secondo libro studia la stabilità dell'equilibrio di segmenti di paraboloide galleggianti. Il problema era stato certamente scelto per l'interesse delle sue applicazioni alla tecnologia navale, ma la sua soluzione ha anche un grande interesse matematico. Archimede studia la stabilità al variare di due parametri, un parametro di forma e la densità, e determina valori di soglia di entrambi i parametri che separano le configurazioni stabili da quelli instabili. Per E.J. Dijksterhuis si tratta di risultati "decisamente al di là del confine della matematica classica". |
 |
|||
Tale forza è detta forza di Archimede o spinta di Archimede o ancora spinta idrostatica (nonostante non riguardi solo i corpi immersi in acqua, ma in qualunque altro fluido – liquido o gas). Una formulazione più semplice del principio è la seguente:
|
||||
Riferimenti
presi da Wikipedia
|
||||
| <<< Indietro |
Formule
Da un punto di vista matematico, la forza di Archimede può essere espressa nel modo seguente:
essendo ρflu la densità (massa volumica) del fluido, g l'accelerazione di gravità e V il volume spostato (che in questo caso è uguale al volume del corpo). Allo stesso modo, il peso del corpo è dato da
essendo ρsol la densità media del solido immerso.
La spinta è indipendente dalla profondità alla quale si trova il corpo.
La densità relativa (del corpo immerso nel fluido rispetto alla densità del fluido) è facilmente calcolabile senza misurare alcun volume:
Densità relativa = {Peso del corpo nello spazio vuoto} / {Peso del corpo nello spazio vuoto - Peso della parte immersa nel fluido}.
Il peso di un corpo immerso (parzialmente o totalmente) non è
quello
totale misurabile fuori dal liquido, ma il peso del volume di fluido
spostato dalla parte immersa. Questa quantità riduce il peso del corpo
(parte immersa e non nel fluido) quando si trova appeso ad un filo
nello spazio vuoto.
Algoritmo del SOFTWARE
Fase 1
|
Funzione per il calcolo della
Massa di Gas in Bombola
|
||
| In | p = Pressione della bombola in Bar | |
| In | V = Il litraggio della bombola in litri | |
| In | T = Temperatura in gradi | |
| In | fO2 = frazione di ossigeno | |
| OUT | Restituisce la massa del gas in bombola in Kg |
Fase 2
|
Funzione per il calcolo della
Massa Totale Gas e Bombola
|
||
| In | Kg = Peso del gas in bombola | |
| In | kg = Peso della bombola Vuota | |
| In | Kg = Peso della rubinetteria | |
| OUT | Kg = Teso totale |
Fase 3
|
Funzione per il calcolo della
Spinta di Archimede
|
||
| In | d = densita' del liquido in Kg/m^3 | |
| In | V = Volume esterno della Bombola in M^3 | |
| OUT | Restituisce forza in [N] se positiva = ascendente |
Fase 4
|
Funzione per scrivere i
risultati
|
||
| OUT | Spinta di Galleggiamento in [N] | |
| OUT | Spinta di Affondamento in [N] | |
| OUT | Risultante della spinta ( Galleggiamento + Affondamento) in [N] | |
| OUT | Spinta di Galleggiamento in [Kg] | |
| OUT | Spinta di Affondamento in [Kg] | |
| OUT | Somma algebrica ( Gallegiamento + Affondamento) in [Kg] |
|
Funzione per il calcolo del volume esterno della Bombola
|
Per quanto concerne la funzione per il calcolo del volume della Bombola ho direttamente riportato il codice sorgente.
- private double Volume_Bombola(int B, int M, int T, int H)
- { // dichiaro le variabili
- double m_B = 0;
- double m_M = 0;
- double m_T = 0;
- double m_H = 0;
- double raggio = 0;
- // trasformo i millimetri in metri
- m_B = ((double)B / 1000);
- m_M = ((double)M / 1000);
- m_T = ((double)T / 1000);
- m_H = ((double)H / 1000);
- // dal diametro ricavo il raggio
- raggio = m_H/2;
- // determino il volume della testa della bombola
- // 1/3*pi*h^2(3r-h)
- double m_punta = 0;
- m_punta = (((1D / 3D) * Math.PI) * (m_T * m_T) * (3D * raggio - m_T));
- // determino il volume della parte centrale della bombola
- double m_cilindro = 0;
- m_cilindro = (Math.PI * Math.Pow(raggio, 2) * m_M);
- // determino il volume del fondo della bombola
- // 1/3*pi*h^2(3r-h)
- double m_fondo = 0;
- m_fondo = (((1D / 3D) * Math.PI) * (m_B * m_B) * (3D * raggio - m_B));
- // Il risultato e' in metri cubi
- return Math.Round((m_punta + m_cilindro + m_fondo),5);
- }
| <<< Indietro |
Contact ::[Email Address]